METODO SEMPLIFICATO PER DETERMINARE FI


Si descrive un metodo semplificato che consente di determinare fi quando questa dipende da piu' elementi reattivi.
Si premette la definizione di capacita' non interagenti : due o piu' condensatori si dicono non interagenti se l'impedenza vista dai morsetti di ciascuno di essi e' puramente resistiva.
Ovviamente nel far cio' si deve eliminare l'effetto dei generatori indipendenti: si devono cortocircuitare i generatori di tensione e aprire quelli di corrente.
Nel nostro esempio C1 e C2 sono " non interagenti ". Valutiamo le resistenze RC1 (fig.3) e RC2 (fig.4) viste da C1 eC2



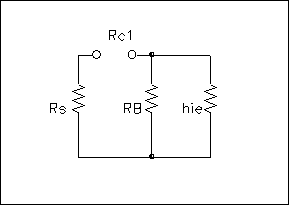
- figura 3 -


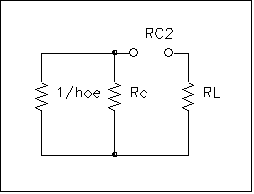
- figura 4 -




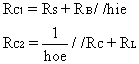
Ciascun condensatore, se agisse da solo, darebbe luogo ad una frequenza di taglio, definita frequenza propria del valore:



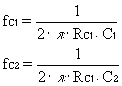
La frequenza di taglio inferiore dipende sia da fC1 che da fC2. Essa,ovviamente, sara' piu' grande della maggiore delle due.

Se fC1=fC2 si ha:

Questa formula deriva da quella piu' generale valida nel caso di n capacita' non interagenti aventi stessa frequenza propria fp:

- formula 4 -




Se, invece, le frequenze proprie sono diverse tra loro si applica la :



Nel caso di piu' frequenze proprie dovute a capacita' non interagenti, la frequenza di taglio inferiore si determina eseguendo la radice quadrata della somma dei quadrati di tutte le frequenze proprie.
Dalla formula precedente si vede che fi coincide, praticamente, con la piu' grande delle frequenze proprie se questa e' di valore almeno quattro volte rispetto all' altra; cioe' :



Infatti nella formula 4 il contributo della frequenza propria piu' grande, essendo il legame matematico del tipo somma di quadrati, e' almeno 16 volte maggiore dell' altra.
La frequenza dominante e' quella proprio piu' grande.


Amplificatore home page